Rumus Interpolasi dan Ekstrapolasi di Tabel Microsoft Excel
Pada dasarnya interpolasi tidak lebih dari pada sebuah upaya menemukan angka-angka yang terdapat ditengah-tengah antara angka terkecil dengan terbesar. Sedangkan untuk menemukan angka-angka yang terdapat diluar angka terkecil dan angka terbesar disebut sebagai ekstrapolasi. Tetapi, sebelum kita mendiskusikan keduanya, mari kita membahas tentang deretan angka, karena pada dasarnya baik ekstrapolasi dan interpolasi berhubungan dengan deretan angka. Bahkan keduanya tidak lebih daripada sekedar deretan angka.
Daftar Isi
Mengenai deretan angka, baik berdasarkan aritmetika, geometri maupun corak atau pola
Deretan angka merupakan sebuah susunan angka yang bermula dari angka terkecil (berapapun itu) sampai dengan angka terbesar, misalnya deretan angka 1,2,3,4,5 merupakan sebuah deretan angka dengan angka 1 sebagai angka terkecil dan 5 sebagai angka terbesar.
Sedangkan deretan angka 4,5,6,7,8 adalah deretan angka dengan angka 4 sebagai angka terkecil dan angka 8 sebagai angka terbesar. Deretan angka diatas memiliki pola setiap angka berikutnya merupakan angka sebelumnya ditambah dengan angka satu. Tetapi, bisa saja sebuah deretan angka tidak memiliki pola sama sekali, seperti pada deretan angka 8,2,45,5,1,9,2.
Deret angka aritmetika
Setiap deretan angka, dimana angka kedua merupakan hasil daripada angka sebelumnya ditambah bilangan tertentu, merupakan deret angka aritmetika, seperti pada contoh berikut ini:
- 8,9,10,11,12,
- Urutan angka:
- Angka pertama = 8,
8 adalah angka terkecil untuk deretan angka ini. - Angka kedua = 9,
- Angka kedua didapatkan dari angka pertama ditambah angka 1,
- 9 = 8 + 1,
- Angka ketiga = 10,
- Angka ketiga didapatkan dari angka kedua ditambah angka 1,
- 10 = 9 + 1,
- Angka keempat = 11,
- Angka keempat didapatkan dari angka ketiga ditambah angka 1,
- 11 = 10 + 1,
- Angka kelima =12,
- Angka kelima didapatkan dari angka keempat ditambah angka 1,
- 12 = 11 + 1,
- Angka pertama = 8,
- Berarti xn=x(n-1)+1,
- Misalkan xn=angka ketiga,
- x(n-1)=angka ketiga-1 (berarti angka kedua),
- Sehingga x_n=x_(n-1)+1=9+1=10
- Urutan angka:
- 1,3,5,7,9,
- Urutan angka:
- Angka pertama = 1,
adalah angka terkecil untuk deretan angka ini. - Angka kedua = 3,
- Angka kedua didapatkan dari angka pertama ditambah angka 2,
- 3 = 1 + 2,
- Angka ketiga = 5,
- Angka ketiga didapatkan dari angka kedua ditambah angka 2,
- 5 = 3 + 2,
- Angka keempat = 7,
- Angka keempat didapatkan dari angka ketiga ditambah angka 2,
- 7 = 5 + 2,
- Angka kelima =9,
- Angka kelima didapatkan dari angka keempat ditambah angka 2,
- 9 = 7 + 2,
- Angka pertama = 1,
- Berarti xn=x(n-1)+2,
- Misalkan x(n-1)=angka kelima
- x(n-1)=angka kelima-1 (berarti angka keempat),
- Sehingga x(n)=x(n-1)+2,=9+2=11
- Urutan angka:
Deret angka geometri
Untuk deretan angka, dimana angka kedua merupakan hasil daripada angka sebelumnya dikalikan dengan bilangan tertentu disebut sebagai deret angka aritmetika, seperti pada contoh berikut ini:
- 2,4,8,16,32,
- Urutan angka:
- Angka pertama = 2,
2 adalah angka terkecil untuk deretan angka ini. - Angka kedua = 4,
- Angka kedua didapatkan dari angka pertama dikali angka 2,
- 4 = 2(2),
- Angka ketiga = 8,
- Angka ketiga didapatkan dari angka kedua dikali angka 2,
- 8 = 4(2),
- Angka keempat = 16,
- Angka keempat didapatkan dari angka ketiga dikali angka 2,
- 16 = 8(2),
- Angka kelima =32,
- Angka kelima didapatkan dari angka keempat dikali angka 2,
- 32 = 16(2),
- Angka pertama = 2,
- Berarti xn=x(n-1)(2),
- Misalkan xn=angka ketiga,
- x(n-1)=angka ketiga-1 (berarti angka kedua),
- Sehingga x(n)=x(n-1)(2)=4(2) = 8
- Urutan angka:
- 1,3,9,27,81,
- Urutan angka:
- Angka pertama = 1,
adalah angka terkecil untuk deretan angka ini. - Angka kedua = 3,
- Angka kedua didapatkan dari angka pertama dikali angka 3,
- 3 = 1(3),
- Angka ketiga = 9,
- Angka ketiga didapatkan dari angka kedua dikali angka 3,
- 9 = 3(3),
- Angka keempat = 27,
- Angka keempat didapatkan dari angka ketiga dikali angka 3,
- 27 = 9(3),
- Angka kelima =81,
- Angka kelima didapatkan dari angka keempat dikali angka 3,
- 81 = 27(3),
- Angka pertama = 1,
- Berarti xn=x(n-1)+2,
- Misalkan x(n-1)=angka ketiga
- x(n-1)=angka ketiga-1 (berarti angka kedua),
- Sehingga xn=x(n-1)(3)=9(3)=27
- Urutan angka:
Deret angka yang memiliki pola atau corak
Nah, sekarang perhatikan angka berikut ini:
- 1,2,5,6,1,2,5,6,1,2,5,6,
- 2,2,4,5,2,2,6,7,
Nah, seperti kita lihat bersama, kedua deretan angka tersebut sama sekali bukanlah deretan angka aritmetika karena tidak ada unsur penambahan untuk setiap angka yang terdapat didalam deretan.
Kedua deretan angka tersebut juga bukanlah deretan angka geometri, karena setiap angkanya bukanlah hasil perkalian antara angka sebelumnya dengan angka tertentu.
Tetapi walaupun begitu, kita menemukan ada sebuah pola atau corak, seperti misalnya:
- Untuk deretan angka pertama, merupakan pengulangan angka-angka 1,2,5,6 yang diulang sebanyak tiga kali. Untuk angka-angka selanjutnya juga merupakan pengulangan dari angka yang sama,
- Untuk deretan angka kedua, hanya sekedar pengulangan angka 2,2 kemudian dilanjutkan dengan angka 4,5. Berikutnya, angka 2,2 diulang lagi kemudian untuk angka ketiga ditambah satu menjadi 5 dan angka berikutnya ditambah satu menjadi 6,
Walaupun untuk deretan angka kedua memiliki unsur penambahan, tetapi tetap tidak termasuk kategori deret angka aritmetika, karena unsur penambahan tidak terdapat di setiap angka, melainkan hanya dua angka setelah angka 2 dan 2.
Interpolasi
Nah, interpolasi seperti kita singgung dibagian pendahuluan, tidak lebih daripada menemukan angka-angka yang terdapat diantara angka terkecil dan terbesar. Misalkan kita memiliki 1 sebagai angka terkecil dan 4 sebagai angka terbesar. Setelah itu kita diminta untuk menemukan dua angka diantara kedua angka terkecil dan terbesar tersebut. Maka jawabannya sangat mudah, yaitu 2 dan 3.
Nah, kitapun juga bisa dengan mudah menggunakan Excel untuk menemukan angka-angka yang terdapat diantara kedua angka terbesar dan terkecil, dengan cara sebagai berikut:
- Angka terkecil ada 11 dan angka terbesar adalah 15,
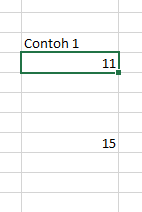
Figure 1 Angka terkecil dan terbesar
- Diantara kedua angka tersebut ada 3 cell yang perlu kita isi,
- Kita harus membuat formula interpolasi, yaitu:
- =(angkaTerbesar – angkaTerkecil) / (ROW(angkaTerbesar) – ROW(angkaTerkecil),
- Mari kita masukkan formula ini di cell B1,

Figure 2 Formula interpolasi untuk contoh 1
- Setelah itu, kita masukkan di cell D5 formula =D4+B2,
- Kemudian kita masukkan di cell D6 formula =D5+B2,
- Kemudian kita masukkan di cell D7 formula =D6+B2,
- Setelah itu kita akan langsung mendapatkan hasilnya dengan tepat,
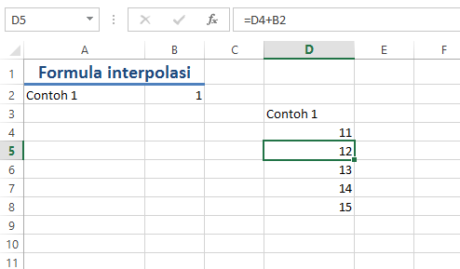
Figure 3 Formula yang sudah kita masukkan akan langsung menghasilkan angka yang tepat
Nah, sekarang mari kita membuat contoh kedua dengan angka 7 sebagai angka terkecil dan 9 sebagai angka terbesar.
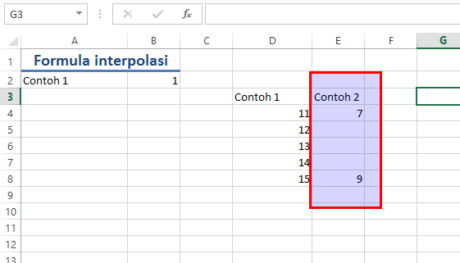
Figure 4 Contoh kedua
Diantara angka 7 dan 9 terdapat 3 cell yang harus kita isi. Langkah-langkahnya adalah sebagai berikut:
- Mari kita memasukkan formula interpolasi di cell B3 dengan formula yang sama persis dengan formula diatas kecuali alamat cell, yaitu =(E8-E4)/(ROW(E8)-ROW(E4)),

Figure 5 Rumus interpolasi kita masukkan ke B3
- Setelah itu, mari kita masukkan di cell E5 formula =E4+B3,
- Setelah itu, mari kita masukkan di cell E6 formula =E5+B3,
- Setelah itu, mari kita masukkan di cell E7 formula =E6+B3,
- Kemudian, kita akan langsung melihat hasilnya,
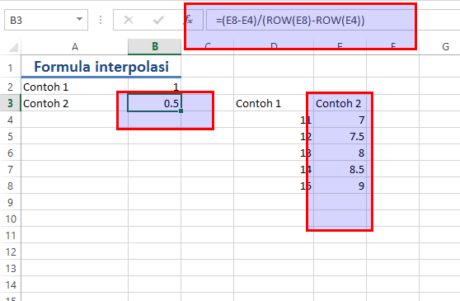
Figure 6 Hasilnya langsung muncul seketika
Mudah bukan?
Ekstrapolasi
Nah, sekarang kita angka-angka diantara angka terkecil dan terbesar dikedua contoh diatas sudah bisa ditemukan, bagaimana caranya menemukan angka diurutan yang sama tetapi lebih besar daripada angka terbesar?
Untuk menemukan angka yang lebih besar daripada angka terbesar disebut sebagai ekstrapolasi. Tetapi rumus yang digunakan untuk ekstrapolasi juga sama persis dengan rumus interpolasi diatas. Sebagai contoh:
- Contoh pertama, mari kita temukan angka yang lebih besar dari angka 15 di cell D9 dan D10,
- Masukkan formula =D8+B2 di cell D9,
- Masukkan formula =D9+B2 di cell D10,
- Maka hasilnya akan langsung terlihat,

Figure 7 Rumusnya sama persis bukan
- Contoh kedua, mari kita temukan kedua angka yang lebih besar dari angka 9 di cell E9 dan E10,
- Masukkan formula =E8+B3 di cell E9,
- Masukkan formula =E9+B3 di cell E10,
- Dan kita akan langsung mendapatkan hasilnya,

Figure 8 Ini dia hasilnya
Jadi, bisa kita simpulkan bahwa rumus interpolasi dan ekstrapolasi di Excel menggunakan formula yang sama.
Topik yang berhubungan
- https://www broexcel com/rumus-interpolasi-dan-ekstrapolasi-di-tabel-microsoft-excel html