Jenis dan Rumus Fungsi Matematika dalam Microsoft Excel
Daftar Isi
Pendahuluan
Eksponensial, akar kuadrat dan Logaritma merupakan ketiga hal yang teramat sangat fundamental didalam dunia Matematika. Tanpa pengetahuan akan ketiganya, maka bisa dipastikan kita akan teramat susah untuk melakukan berbagai ragam kalkulasi aritmetika maupun menyelesaikan beragam persamaan Matematika. Oleh karena itu, sebelum kita membahas “fungsi” Matematika, kita akan terlebih dahulu membahas ketiga hal tersebut terlebih dahulu. Microsoft excel memiliki kemampuan untuk menjawab semua fungsi matematika yang kita perlukan.
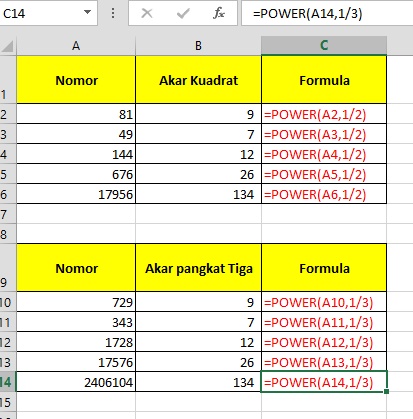
Mengenai eksponensial dan akar kuadrat
Eksponen pada dasarnya merupakan bentuk perkalian, hanya saja disini perkalian tersebut dilakukan dengan dirinya sendiri. Sebagai contoh:
2^2=2(2)=4
2^3=2(2)(2)=4(2)=8
2^4=2(2)(2)(2)=4(2)(2)=8(2)=16
Diatas angka dua, kita menjumpai bilangan berpangkat 2, 3 dan 4. Itu adalah sebuah simbol yang menunjukkan bahwa kita harus mengalikan angka 2 dengan pangkat bilangan tersebut. Mari kita mencoba menghitung beberapa contoh tambahan dibawah ini.
3^5=3(3)(3)(3)(3)=9(3)(3)(3)=27(3)(3)=81(3)=243
10^3=10(10)(10)=100(10)=1000
Eksponensial dengan angka negatif
Bagaimana dengan angka negatif atau minus? Apakah eksponensial juga bisa digunakan untuk angka negatif?
-3^2=3(3)=9=-9
-2^3 (4)-10=2(2)(2)(4)-10=-8(4)-10=-32-10=-22Disini yang perlu diperhatikan adalah ketika kita melakukan eksponensial dengan angka negatif, perkalian haruslah dilakukan terlebih dahulu tanpa memperhatikan apakah angka tersebut negatif atau positif. Oleh karena itu bukan 9. Perhatikan bedanya:
〖-3〗^2=3(3)=9 →-9
-3(-3)=9
Dari dua contoh diatas terlihat bedanya bukan? Untuk perkalian eksponensial, 3 haruslah dikalikan dengan 3 terlebih dahulu, kemudian hasilnya harus dijadikan negatif. Sedangkan perkalian negatif tanpa eksponen, maka hasilnya akan menjadi positif karena negatif X negatif = positif.
Kemudian, kita juga bisa melakukan beragam operasional aritmetika dengan eksponensial juga, seperti contoh dibawah ini.
4^2 (5)+3=16(5)+3=80+3=83
6(3^2 )(2^3 )=6(9)(8)=54(8)=432
Eksponsial dengan variable
Nah, selain langsung menggunakan angka, eksponensial juga bisa digunakan untuk melakukan kalkulasi pada variable. Sebagai contoh:
x^2=x(x)
x^4=x(x)(x)(x)
y^2=y(y)
Sebagai tambahan, mari kita diskusikan beberapa soal berikut ini:
- Hitunglah x^2 bila diketahui x=10,
- x^2=〖10〗^2=10(10)=100
- Hitunglah x^3 (y^2 )+x-y dengan x=10, y=3,
- x^3 (y^2 )+x-y=〖10〗^3 (3^2 )+10-3=1000(9)+7=9000+7=9007
Mengenai akar sebagai kebalikan dari operasi eksponensial
Sebetulnya akar merupakan kebalikan dari eksponen. Bilamana eksponen merupakan perkalian dengan dirinya sendiri, akar merupakan upaya untuk mencari faktor yang digunakan untuk perkalian. Akar menggunakan simbol .
Sebagai contoh, mari kita menghitung beberapa eksponensial sederhana dibawah ini:
3^2=3(3)=9
4^3=4(4)(4)=16(4)=64
Nah, dari perhitungan diatas dengan jelas kita mengetahui bahwa menghasilkan nilai 9 dan untuk menghasilkan nilai 64. Nah sekarang bagaimana dengan akar dari kedua nilai tersebut?
√9=3
∛64=4
Mudah dimengerti bukan? Jadi memang akar merupakan seratus persen kebalikan dari eksponensial. Hanya saja, memang tanpa menggunakan kalkulator sangat susah untuk menghitung faktor-faktor dari sebuah akar. Bilamana bentuk eksponen 4^3 dengan mudah kita temukan jawabannya, karena memang hanya sekedar mengalikan 4 selama tiga kali, tetapi ∛64 relatif susah untuk ditemukan jawabannya.
Mengenai akar kuadrat
Seringkali kita menemukan istilah akar kuadrat, tetapi apakah gerangan akar kuadrat ini? Sebetulnya, setiap akar dengan faktor dua selalu disebut dengan akar kuadrat, seperti √(9) dan √(16). Nah, untuk faktor dua, atau yang disebut dengan akar kuadrat ini, biasanya angka yang menunjukkan jumlah faktor sama sekali tidak dituliskan. Oleh karena itu untuk 2√(9) lebih sering ditulis √9. Untuk 2√(16) lebih sering ditulis dengan √16.
Mengenai Logaritma sebagai bagian dari eksponensial dan akar
Kenapa Logaritma disebut sebagai bagian dari eksponensial dan akar? Hal ini dikarenakan Logaritma merupakan sebuah upaya untuk menemukan pangkat dari sebuah bilangan yang telah dikalkulasikan secara eksponensial. Mari kita diskusikan beberapa contoh:
- 3^2
- Bentuk eksponen 3^2=3(3)=9,
- Bentuk akar √9=3 karena 3(3)=9,
- Bentuk Logaritma Log3 (9)=2 karena 3^2=9,
- 4^2
- Bentuk eksponen 4^2=4(4)=16,
- Bentuk akar √16=4 karena 4(4)=16,
- Bentuk Logaritma Log4 (16)=2 karena 4^2=16,
Oleh karena itu, bentuk-bentuk dari eksponensial, akar dan Log adalah sebagai berikut:
- Eksponensial -> menghitung bilangan berpangkat,
- Akar -> mencari bilangan yang telah dipangkatkan,
- Logaritma -> mencari pangkat dari hasil eksponensial
Mengenai variable
Sebetulnya, didalam dunia matematika, setiap jenis perhitungan lebih sering ditulis dalam bentuk variable daripada langsung dengan angka. Hal ini membuat perhitungan jauh lebih mudah untuk diaplikasikan kedalam beragam jenis angka.
Perhatikan contoh perhitungan-perhitungan dibawah ini:
- 10(2)+3(4)=20+12=32
- 3^2 (4)+5(2^2 )=9(4)+5(4)=36+20=56
Kedua perhitungan diatas langsung menggunakan angka. Oleh karena itu, setiap perhitungan diatas merupakan perhitungan yang sangat spesifik dengan angka-angka tertentu. Dengan penggunaan variable, kita akan menjadi jauh lebih mudah untuk melakukan perhitungan yang sama dengan angka berapapun juga.
Mari kita rubah kedua perhitungan diatas kedalam bentuk variable:
- x(m)+y(n)
- x^2 (m)+y(n^2)
Nah, disini kita bisa menggunakan angka berapapun juga untuk kedua formula aljabar diatas. Nah, mari kita jabarkan perhitungan aljabar ini menggunakan perhitungan diatas:
- x(m)+y(n)
- x=10
- y=3
- m=2
- n=4
- x(m)+y(n)=10(2)+3(4)=20+12=32
- x^2 (m)+y(n^2 )
Setelah mempelajari kalkulasi nomor satu diatas, silahkan mengerjakan soal nomor dua ini dengan menggunakan angka-angka diatas.
Mengenai persamaan
Persamaan tidak lebih daripada sekedar pernyataan bahwa . Disini, kita menggunakan simbol = untuk menyatakan bahwa x sama dengan y. Sebagai contoh:
- 5=5,
- 5+2=7,
Disini kita menyatakan bahwa 5+2 nilainya sama dengan 7. Apakah 5+2 sama dengan 7? Benar atau salah? - 5^2=5(5)=25,
Nah, untuk ini, kita menyatakan bahwa 52 nilainya sama dengan 5(5) dan nilainya juga sama dengan 25. Apakah betul?
Persamaan kuadrat atau quadratic equation
Setelah memahami eksponensial, akar dan penggunaan variable, sekarang kita sudah siap untuk membahas persamaan kuadrat atau quadratic equation. Banyak orang menggunakan istilah rumus abc untuk mengacu ke persamaan kuadrat ini.
Persamaan kuadrat mengacu kepada bentuk ax^2+bx+c=0. Disini, berapapun angka disebelah kiri tanda sama dengan, ketika dikalkulasikan, hasilnya selalu 0. Dengan kata lain, ax^2+bx+c hasilnya harus selalu 0.
Sebagai contoh, x^2+3x-4=0 merupakan sebuah persamaan kuadrat. Disini kita perlu mencari nilai x untuk melengkapi persamaan tersebut, sehingga kita bisa mengecek apakah hasilnya benar 0 atau tidak. Oleh karena itu, persamaan kuadrat merupakan sebuah upaya untuk mencari nilai kedua x guna melengkapi persamaan.
Untuk mencari nilai kedua x yang belum diketahui, kita bisa menggunakan formula (-b±√(b^2-4ac))/2a. Mari kita gunakan formula ini untuk mencari tahu kedua nilai x didalam persamaan x^2+3x-4=0:
(-b±√(b^2-4ac))/2a
=(-3±√(3^2-4(1)(-4)))/(2(1))
=(-3±√(9+16)))/(2(1))
=(-3±√(25)))/(2(1))
=(-3±5)/2
=(-3-5)/2=(-8)/2=-4 dan =(-3+5)/2=2/2=1
Setelah kita menemukan bahwa kedua x nilainya -4 dan 1, mari kita masukkan kedua nilai ini kedalam persamaan diatas:
- x=-4
x^2+3x-4=0
〖-4〗^2+3(-4)-4=0
-16-12-4=0
-4-4=0
0=0 - x=1
x^2+3x-4=0
1^2+3(1)-4=0
1+3-4=0
4-4=0
0=0
Sangat sederhana bukan?
Mengenai konsep “fungsi” dalam Matematika
Kita sudah membahas mengenai variable untuk menggantikan angka sehingga sebuah formula bisa digunakan untuk beragam angka yang kita butuhkan. Diatas kita sudah mendiskusikan formula . Nah sekarang, bagaimanakah caranya untuk memasukkan angka kedalam formula tersebut?
Untuk memasukkan angka kedalam formula aljabar, kita menggunakan sebuah konsep yang dinamakan sebagai function atau fungsi dengan notasi f(x,y,m,n)=x(m)+y(n). Nah, mari kita mencoba untuk menggunakan fungsi ini untuk berbagai angka:
- x=7, y=4, m=2, n=5,
f(x,y,m,n)=x(m)+y(n)
f(7,4,2,5)=x(m)+y(n)
f(7,4,2,5)=7(2)+4(5)=14+20=34 - x=2, y=3, m=1, n=9,
f(x,y,m,n)=x(m)+y(n)
f(2,3,1,9)=x(m)+y(n)
f(2,3,1,9)=2(1)+3(9)=2+27=29 - x=1, y=3, m=6, n=6,
f(x,y,m,n)=x(m)+y(n)
f(1,3,6,6)=1(6)+3(6)
f(2,3,1,9)=6+18=24
Notasi fungsi diatas merupakan notasi fungsi Matematika yang paling umum. Masih ada satu lagi notasi fungsi Matematika yang disebut sebagai Lambda Calculus. Sebetulnya Lambda Calculus merupakan sesuatu hal yang cukup komplek.
Tetapi barangkali ada seorang atau dua orang pembaca yang penasaran bagaimana menuliskan ketiga fungsi diatas kedalam Lambda Calculus, maka penulis memutuskan untuk memberikan contoh pertama kedalam notasi Scheme (salah satu bahasa pemrograman yang mengimplementasikan Lambda Calculus).
f(x,y,m,n)=x(m)+y(n)
(lambda (x y m n)
(+ (* x m)
(* y n)))
Bilamana fungsi Lambda Calculus diatas terlihat rumit, janganlah kuatir, karena memang perlu waktu untuk memahami bidang ini. Jadi, anggap saja fungsi diatas merupakan perkenalan kedalam dunia Lambda Calculus.